MathType - The #Gradient descent is an iterative optimization #algorithm for finding local minimums of multivariate functions. At each step, the algorithm moves in the inverse direction of the gradient, consequently reducing
Por um escritor misterioso
Descrição
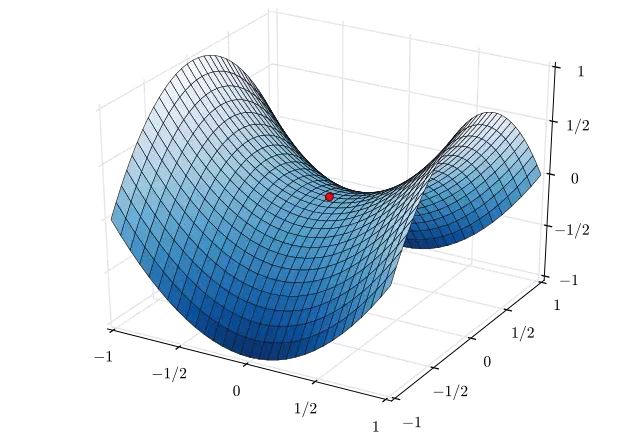
Gradient Descent Algorithm
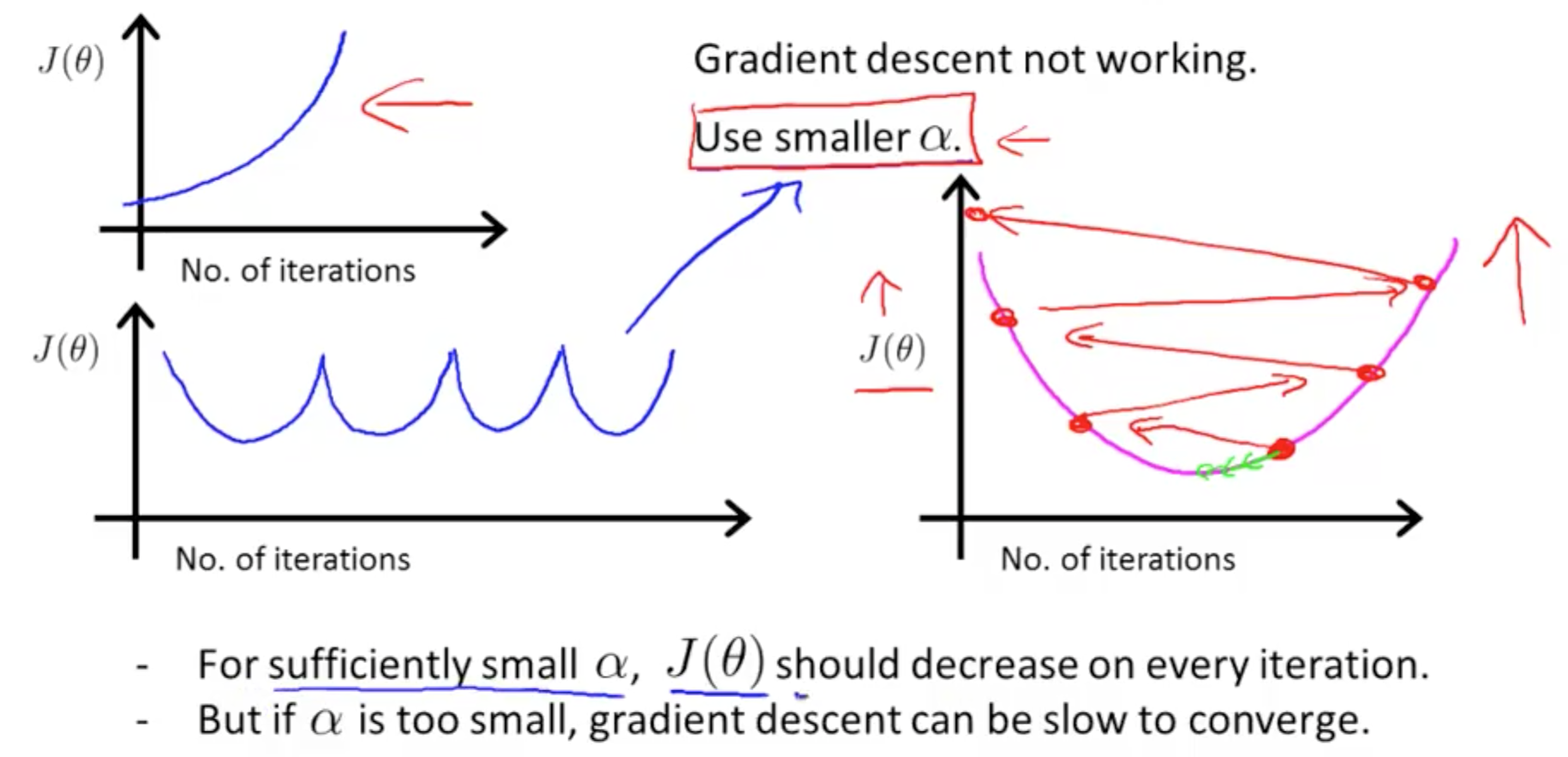
Linear Regression with Multiple Variables Machine Learning, Deep Learning, and Computer Vision

machine learning - Java implementation of multivariate gradient descent - Stack Overflow
Optimization Techniques used in Classical Machine Learning ft: Gradient Descent, by Manoj Hegde
Is there a mathematical proof of why the gradient descent algorithm always converges to the global/ local minimum if the learning rate is small enough? - Quora

Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. To find a local minimum of a function using gradient descent, we take steps proportional

Gradient descent optimization algorithm.
Can gradient descent be used to find minima and maxima of functions? If not, then why not? - Quora
In mathematical optimization, why would someone use gradient descent for a convex function? Why wouldn't they just find the derivative of this function, and look for the minimum in the traditional way?

L2] Linear Regression (Multivariate). Cost Function. Hypothesis. Gradient

Can gradient descent be used to find minima and maxima of functions? If not, then why not? - Quora
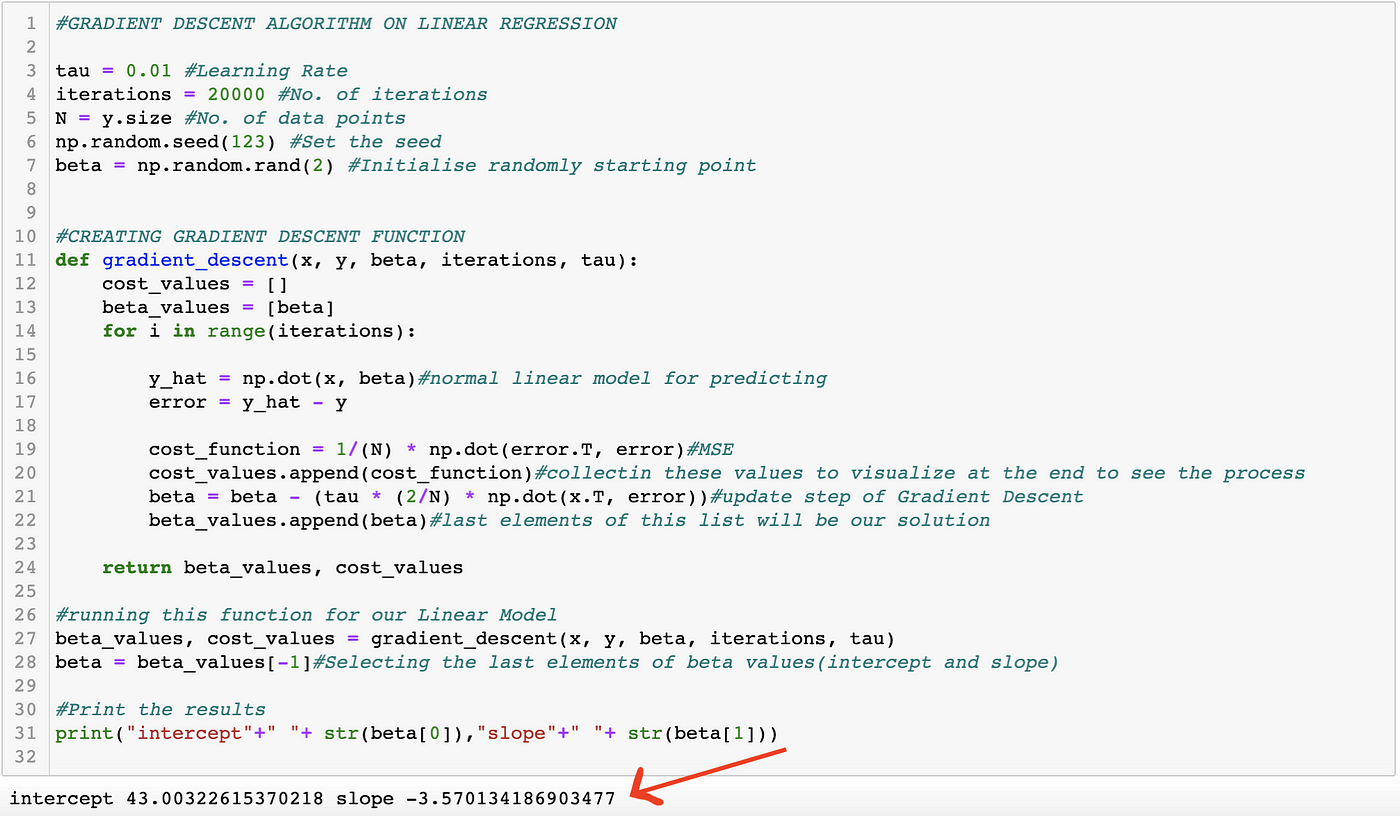
Explanation of Gradient Descent Optimization Algorithm on Linear Regression example., by Joshgun Guliyev, Analytics Vidhya

Conditional gradient method for multiobjective optimization

Gradient Descent algorithm. How to find the minimum of a function…, by Raghunath D
de
por adulto (o preço varia de acordo com o tamanho do grupo)







