Casa
four square theorem

PDF) Quarternions and the Four Square Theorem

Por um escritor misterioso

Descrição
The Four Square Theorem was proved by Lagrange in 1770: ev- ery positive integer is the sum of at most four squares of positive integers, i.e. n = A2 +B2 +C2 +D2;A;B;C;D 2 Z An interesting proof is presented here based on Hurwitz integers, a subset
PDF) Quarternions and the Four Square Theorem
Topics in Quaternion Linear Algebra
PDF) Quarternions and the Four Square Theorem
PDF) Quarternions and the Four Square Theorem
PDF) Quarternions and the Four Square Theorem
PDF) Lagrange's Four-Square Theorem
PDF) Quarternions and the Four Square Theorem
The (Imaginary) Numbers at the Edge of Reality
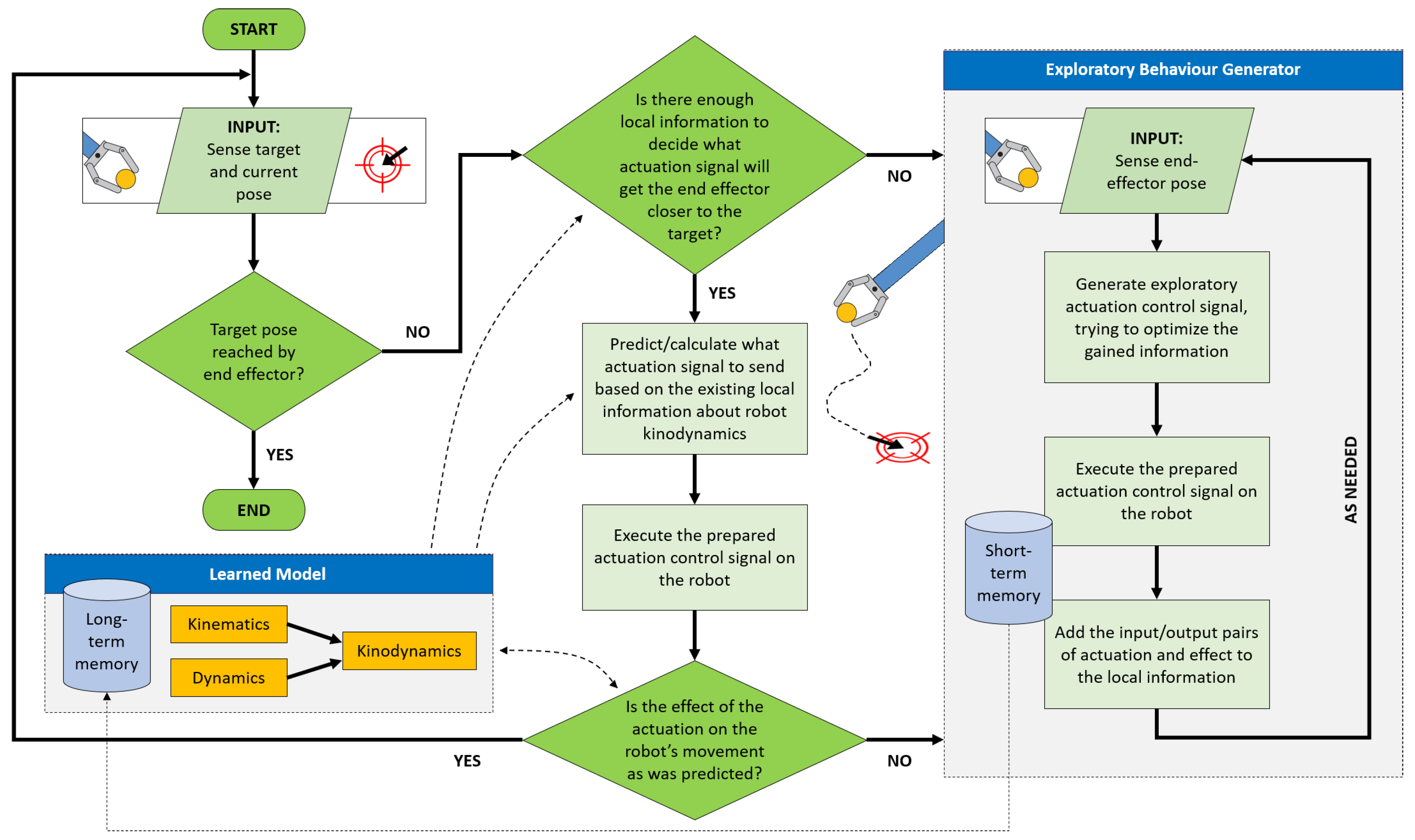
PDF) Quarternions and the Four Square Theorem
Robotics, Free Full-Text
PDF) Quarternions and the Four Square Theorem
Computing the Rotational Diffusion of Biomolecules via Molecular Dynamics Simulation and Quaternion Orientations
PDF) Quarternions and the Four Square Theorem
Number Theory Revealed: A Masterclass
PDF) Quarternions and the Four Square Theorem
On Real Matrices to Least-Squares g-Inverse and Minimum Norm g-Inverse of Quaternion Matrices
PDF) Quarternions and the Four Square Theorem
PDF) Algebraic Consequences of Jacobi's Two- and Four-Square Theorems
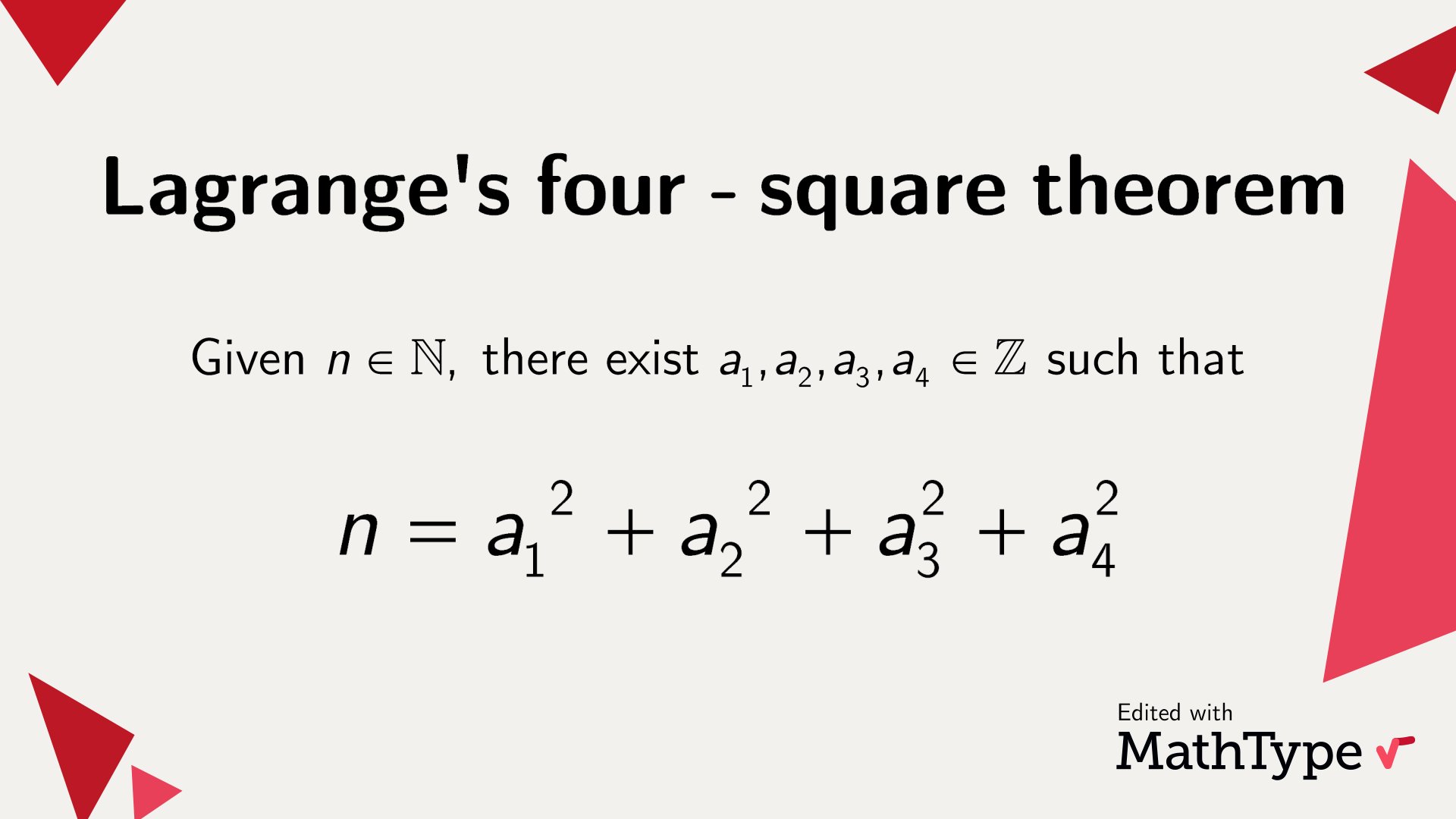
PDF) Quarternions and the Four Square Theorem
MathType on X: Lagrange's four-square theorem asserts that any positive whole number can be written as the sum of four squares of integers. Leave an example in the comments! #MathType #NumberTheory #math #
PDF) Quarternions and the Four Square Theorem
Solving Sums of Squares in Global Fields Proceedings of the 2022 International Symposium on Symbolic and Algebraic Computation
PDF) Quarternions and the Four Square Theorem
Quaternion algebra
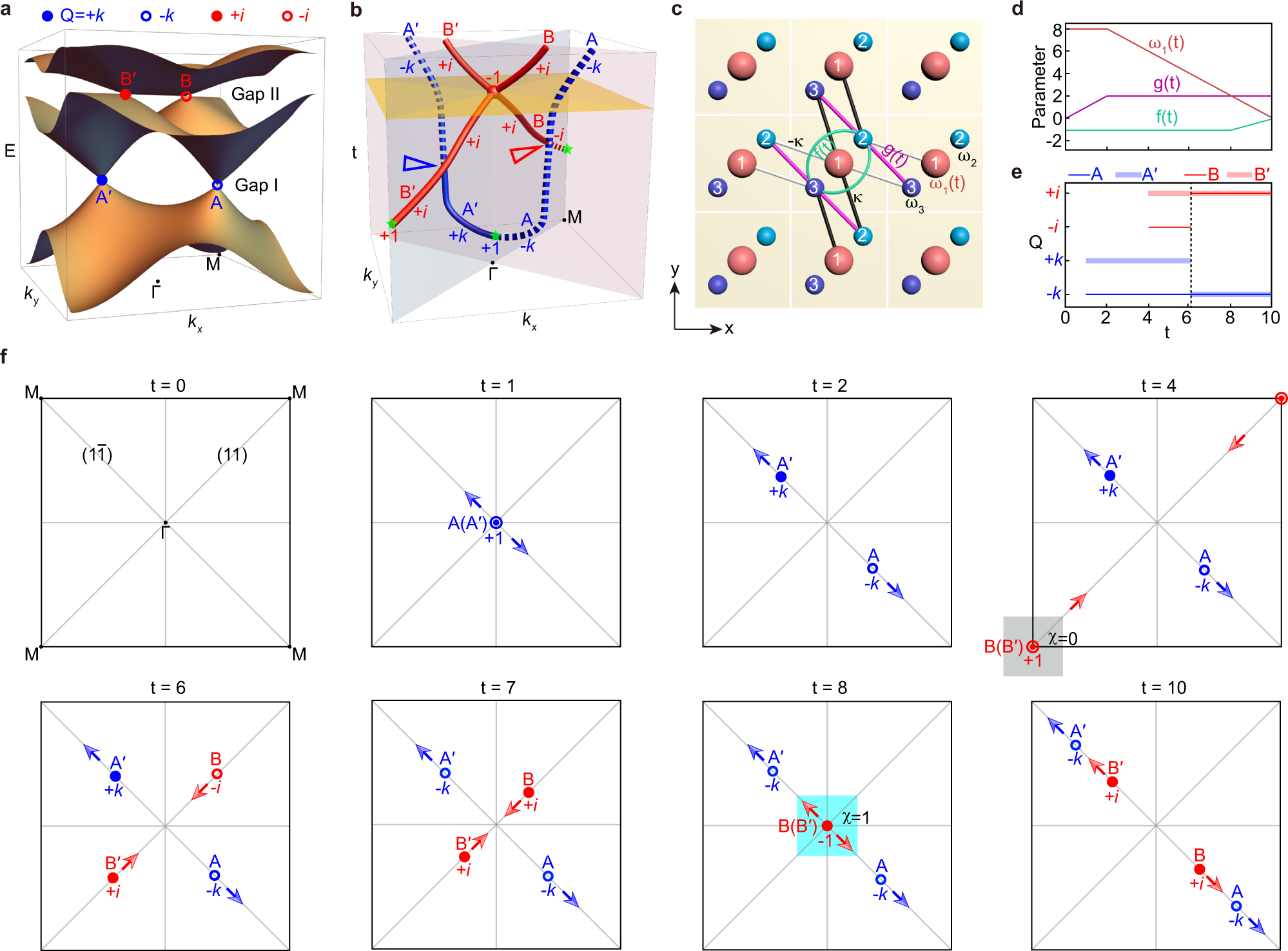
PDF) Quarternions and the Four Square Theorem
Minimal non-abelian nodal braiding in ideal metamaterials
de por adulto (o preço varia de acordo com o tamanho do grupo)