Sum of Squares Function -- from Wolfram MathWorld
Por um escritor misterioso
Descrição
The number of representations of n by k squares, allowing zeros and distinguishing signs and order, is denoted r_k(n). The special case k=2 corresponding to two squares is often denoted simply r_2(n)=r(n) (e.g., Hardy and Wright 1979, p. 241; Shanks 1993, p. 162). For example, consider the number of ways of representing 5 as the sum of two squares: 5 = (-2)^2+(-1)^2 (1) = (-2)^2+1^2 (2) = 2^2+(-1)^2 (3) = 2^2+1^2 (4) = (-1)^2+(-2)^2 (5) = (-1)^2+2^2 (6) = 1^2+(-2)^2 (7) =

Sum of Squares Function -- from Wolfram MathWorld
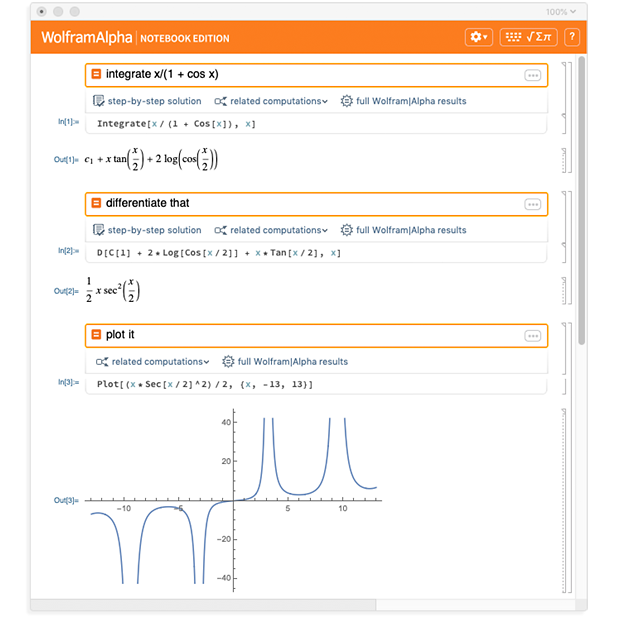
The Ease of Wolfram, Alpha, the Power of Mathematica: Introducing Wolfram

Making Formulas… for Everything—From Pi to the Pink Panther to Sir Isaac Newton—Wolfram

Wolfram MathWorld - Murat Alper

Sum of Squares Function -- from Wolfram MathWorld

Sum of Squares Function -- from Wolfram MathWorld

Sum of Squares Function -- from Wolfram MathWorld
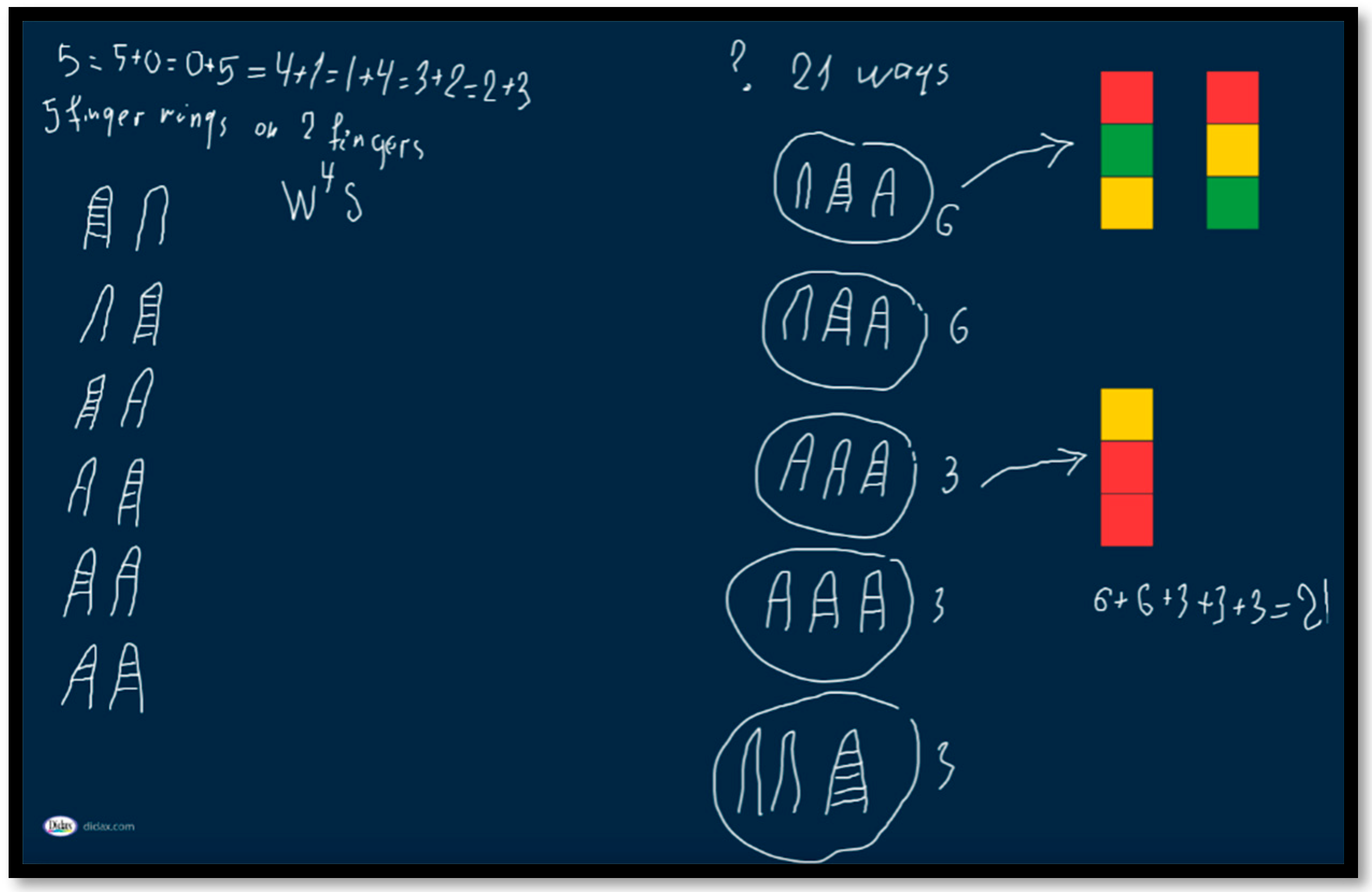
Mathematics, Free Full-Text
de
por adulto (o preço varia de acordo com o tamanho do grupo)







